SNEKMAZE: a cellular automaton
In the process of learning PICO-8, I came across an unexpectedly interesting cellular automaton. I call it SNEKMAZE.

The rules
- There is an NxN maze made of cells that are diagonal lines, either
\or/. (Note that this maze has no branching paths.) - The maze is a torus: it wraps from top to bottom and left to right.
- There is a snake moving through the maze, following the path.
- Whenever the snake enters a cell, the cell farthest from it flips direction.
One possible initial state is that the snake is in the bottom left corner and all the cells are /.
With a maze so simple, and with no randomness, you'd think that it would end up in a loop quickly. But every state has only one possible previous state, so a short loop has no way into it except to already be in the loop. This, and the self-modifying behavior of the maze, results in a chaotic path that takes a very long time to loop.
@Valkhiya on Twitter found that the 8x8 SNEKMAZE goes through 450,160 states before it loops back to the initial state.
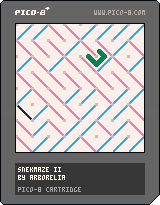
The PICO-8 cartridge
PICO-8 by Lexaloffle is an 8-bit game development system, a "fantasy console" that's designed to be easier and more fun to program than any real system architecture that's ever existed.
One neat feature of PICO-8 is its "cartridges", which are just small image files. A cartridge looks like a screenshot of a program, but it can be loaded in a PICO-8 interpreter and actually contains the whole program.
Here's the cartridge for SNEKMAZE. It's also a link to the code in plain text.
The code
-- snekmaze ii
-- by arborelia
function _init()
-- tiles to move per frame
-- don't make this more than 1
fstep = 1/6
-- step counter
-- it can overflow, that's fine
step = 0
trailpos = 0
-- number of frames in trail
ntrail = 20
-- size of the grid (even)
gsize = 10
-- where to go in the tile
enterx = -1
entery = 0
exitx = 0
exity = -1
-- which tile we're in
tx = 0
ty = 0
grid = {}
local x,y,i
for x=0,gsize-1 do
grid[x] = {}
for y=0,gsize-1 do
grid[x][y] = 0
end
end
-- size of each tile
tsize = flr(128/gsize)
border = (128 - tsize*gsize)/2
camera(-border,-border)
-- trail of prev. locations
trail = {}
trail.x = {}
trail.y = {}
for i=0,ntrail-1 do
trail.x[i] = 0
trail.y[i] = 0.5
end
-- draw starting grid
cls(7)
for x=0,gsize-1 do
for y=0,gsize-1 do
draw_tile(x,y)
end
end
flip_tile()
end
-- run updates at 60 fps
function _update60()
-- previous step
p_step = step
step += fstep
if flr(step) != flr(p_step) then
enter_tile()
end
trailpos = (trailpos + 1) % ntrail
update_trail()
end
function enter_tile()
old_fx = fx
old_fy = fy
enterx = -exitx
entery = -exity
tx = (tx+exitx) % gsize
ty = (ty+exity) % gsize
local way = grid[tx][ty]
if enterx == 0 then
exity = 0
exitx = entery * (1-(2*way))
else
exitx = 0
exity = enterx * (1-(2*way))
end
flip_tile()
draw_tile(old_fx, old_fy)
end
function flip_tile()
-- which tile's being flipped
-- (global)
fx = (tx + gsize/2) % gsize
fy = (ty + gsize/2) % gsize
grid[fx][fy] = 1-grid[fx][fy]
end
function update_trail()
local half=tsize/2
local frac = step - flr(step)
local unfrac = 1-frac
local posx = (
tsize*tx + half
+ half * unfrac * enterx
+ half * frac * exitx
)
local posy = (
tsize*ty + half
+ half * unfrac * entery
+ half * frac * exity
)
trail.x[trailpos] = posx
trail.y[trailpos] = posy
end
function _draw()
local p = trailpos
local n = ntrail
draw_tile(fx,fy)
spot(
trail.x[(p+1) % n],
trail.y[(p+1) % n],
7
)
spot(
trail.x[(p+2) % n],
trail.y[(p+2) % n],
7
)
spot(
trail.x[(p-1) % n],
trail.y[(p-1) % n],
3
)
spot(
trail.x[p],
trail.y[p],
3
)
-- debug()
end
function spot(x,y,c)
local size=flr(tsize/8)
if size < 2 then
rectfill(x,y,x+1,y+1,c)
else
circfill(x,y,tsize/8,c)
end
end
function draw_tile(x,y)
local xin,yin,xout,yout,way,c
rectfill(
x*tsize, y*tsize,
(x+1)*tsize,
(y+1)*tsize,
7
)
way=grid[x][y]
-- where the gate goes, in
-- tile coordinates
xin=x
xout=(x+1)
yin=(y+(1-way))
yout=(y+way)
if way==0 then c=12 else c=14 end
-- is it the flipping tile?
if x==fx and y==fy then
frac = step - flr(step)
if way==1 then
yin=(y+(1-frac))
yout=(y+frac)
else
xin=(x+(1-frac))
xout=(x+frac)
end
-- change line color
c=1
end
if tsize > 8 then
-- draw a thick line
for dx=-1,1 do
for dy=-1,1 do
local pxin = xin*tsize + dx
local pyin = yin*tsize + dy
local pxout = xout*tsize+dx
local pyout = yout*tsize+dy
pxin=mid(x*tsize, (x+1)*tsize, pxin)
pyin=mid(y*tsize, (y+1)*tsize, pyin)
pxout=mid(x*tsize,(x+1)*tsize, pxout)
pyout=mid(y*tsize,(y+1)*tsize, pyout)
line(pxin,pyin,pxout,pyout,c)
end
end
else
line(
xin*tsize,yin*tsize,
xout*tsize,yout*tsize,c
)
end
draw_grid()
end
function draw_grid()
local x,y
for x=0,gsize-1 do
for y=0,gsize-1 do
px = x * tsize
py = y * tsize
if tsize > 8 then
rectfill(px-1,py-1,px+1,py+1,6)
else
pset(px,py,6)
end
end
end
end
function debug()
rectfill(0,0,128,6,0)
print(step,0,0,7)
end